Entry 31: Instruction decoder part 1

Setting up ROM to hold control signals

In the previous section, we created "ROM256x16". The data stored in this ROM is to be control signals for the control pins. In entry 29, we concluded  that we needed a total of 13 control signals / control pins in order to design the simplest possible processor, capable of running the example program that adds 2 numbers. I arbitrarily assign them as follows:

Our ROM has 16 data bits. Bits 13, 14, and 15 are therefore not used at the moment. 

For example, if we have the following data at a given address:

        0011 0000 0000 0000 (Hex 3000)

where bit 2 and bit 3 are high, the decoder will interpret this to mean that PCW = 1 and MARL = 1, that is, the program counter (PC) writes to the address bus and the memory address register (MAR) loads from the data bus (see entry 29). When the clock goes low-to-high, the PC is transferred to MAR. If all bits are 0, no control pin is activated, and nothing happens.

So, we simply connect 13 of the 16 output pins of the ROM to the corresponding control pin:

Let's program ROM so that we have the control signals for T-state 1 at address 0 and the control signals for T-state 2 at address 1. In entry 29, we concluded that

• T-state 1: PCW = 1 and MARL = 1.
• T-state 2: RAMW = 1, IRL = 1, COUNT = 1 (instruction to the instruction register (IR), increment PC).

Therefore, the first two rows of our RAM will contain the following data:

• If we set the ROM address to 0, it will output the correct control signals for T-state 1.
• If we set the ROM address to 1, it will output the correct control signals for T-state 2

There is no "universal" T-state 3, the control signals for T-state 3 depend on the instruction, the opcode that is in the IR when T-state 2 is completed. In entry 29, we figured out the control signals for all instructions in all T-states:

I will fill ROM with these control signals:

• At address 2, all bits are 0, consistent with NOP "no operation" (see entry 28). An address with all data bits equal to 0 is labeled "padding".
• At address 3, we have the control signals for T-state 3 of the instruction LDA. It will move the PC to MAR
• At address 4, we have the control signals for T-state 4 of the instruction LDA. It will move the content of RAM to the A register and increment count.
• At address 5, we have a "padding". When the instruction decoder reads all zeros, it is supposed to interpret this as "the end of the instruction". The decoder is then supposed to change the ROM address to 0, restarting T-state 1.
• Address 6 and 7 deals with the instruction "ADD" (ALU writes the sum, A loads).
• Address 8-11 (hex) deals with the remaining instructions. Address 12 and onwards is unused.
• Note that there are no entries for HLT (halt the program). HLT is not an instruction that requires control pins to be set. I will figure out how to handle HLT later.

Creating an instruction decoder

So, this is what we need to do in order to create an instruction decoder.

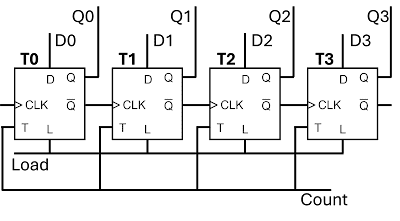
• First, we need a counter to keep track of which ROM address we are currently pointing to. Let's call the counter a "micro counter" to distinguish it from the "program counter", see entry 26.
• Since ROM has an 8 bit address with 256 possible addresses, the micro counter must be an 8 bit counter, counting from 0 to 255 (0 to FF in hex).

• When the "computer" starts, the micro counter should be equal to 0, pointing to address 0. The control signals are then consistent with T-state 1.
• When the clock signal goes high-to-low (falling edge), it should increment (this is different from the program counter, which increments on the rising edge).

• The first time the clock goes high-to-low, the micro counter increments to 1, pointing to T-state 2.
• The second time the clock goes high-to-low, the micro counter increments to 2. 
• When the micro counter is equal to 2, it points to NOP, which is not correct (unless the first instruction happens to be a NOP)
• Therefore, whenever the micro counter is equal to 2, a new value needs to be loaded into the micro counter.
• What value to load depends on the instruction.
• We need to load the address of T-state 3 of the particular instruction (which currently resides in the instruction register, due to the completion of T-state 1 and 2).
• For example, if the instruction is "STA", the micro counter should become equal to 8, pointing to T-state 3 of STA:

• The third time the clock goes high-to-low, the micro counter increments to 9, pointing to T-state 4 of STA. 
• The fourth time the clock goes high-to-low, the micro counter increments to A (10), pointing to the "padding" of STA. When all output signals are 0, the micro counter should reset:

• The cycle starts over again, with T-state 1 followed by T-state 2, fetching the next instruction.

This leaves us with two tasks:

• When the micro counter outputs the number 2, it need to "load itself" with a new address, an address that depends on the instruction in the IR.
• When all output pins of ROM are 0, we need to trigger a reset of the micro counter.

In addition, we must figure out how to handle HLT.. all in the next entry.

Entry 30: ROM and instruction decoding

ROM

"Could you tell me a bit more about ROM and how it is designed internally? I suppose that it cannot be built from D latches like RAM." Even though the answer is probably not that important, I found the answer interesting so I am posting it.

Grok:

Your question about how ROM (Read-Only Memory) is designed internally, and why it can’t be built from D latches like RAM, is a great one! It shows you’re diving deep into the nuts and bolts of your 4-bit processor project. Since you’re considering a ROM-based instruction decoder to store control signals (based on T-states and opcodes), understanding ROM’s internal design will help clarify how it fits into your system and why it’s distinct from RAM. I’ll explain ROM’s purpose, contrast it with RAM, dive into its internal architecture (focusing on mask ROM, PROM, EPROM, and EEPROM for context), and address why D latches aren’t used. I’ll keep it concise yet detailed, tying it to your project where possible, and avoid speculative details since you’ve asked for a factual rundown.

---

What is ROM?

ROM is a type of non-volatile memory that stores fixed data, readable during operation but not typically writable (or only writable under special conditions, unlike RAM). In your case, the ROM will store control signals for each T-state and opcode combination, acting as a lookup table for your instruction decoder.

Key Traits:

• Read-Only (Mostly): Data is preset (e.g., programmed into an EEPROM) and read via address lines (T-state + opcode → signals).
• Non-Volatile: Retains data without power, unlike your RAM (volatile, loses data when powered off).
• Use in Your Project: A ROM (e.g., 256 × 16 bits) maps 8-bit addresses to 16-bit control signals.

Contrast with RAM:

• RAM (e.g., 74LS189): Volatile, read/write, stores program/data (e.g., opcodes at 0000–0111, data at 1000–1111). Uses D latches/flip-flops to hold bits dynamically.
• ROM: Non-volatile, read-only (or rarely writable), stores fixed control logic. Doesn’t use latches, as data is physically encoded.

---

Why ROM Can’t Use D Latches Like RAM?

Your intuition is correct—ROM doesn’t rely on D latches (or flip-flops) like RAM does. Here’s why:

• RAM’s Design (e.g., 74LS189):
  • Storage: Each bit is stored in a memory cell, typically a D latch or SRAM cell (cross-coupled inverters forming a flip-flop, ~6 transistors in CMOS).
  • Dynamic: Latches hold state as long as power is on, changeable via writes.
  • Your: 16 locations × 4 bits, each bit a latch, volatile (loses data without VCC).
• ROM’s Design:
  • Storage: Bits are hardwired or programmed into the physical structure (e.g., metal connections, fuses, or charge traps), not stored dynamically in latches.
  • Operation:
    • Address selects a word (row), and the ROM outputs predefined bits (e.g. one for each control signal).
    • No write circuitry (except in PROM/EPROM/EEPROM, which use special programming).
  • Fixed Data: No need for latches, as bits are encoded permanently (or semi-permanently in EEPROM).
  • Why No Latches?
    • Purpose: ROM stores immutable data (your control signals), so dynamic storage (latches) is unnecessary and power-hungry.
    • Volatility: Latches lose data without power, defeating ROM’s non-volatile goal.
    • Complexity: Latches need write logic and refresh (in DRAM), while ROM uses simpler, static structures (e.g., diodes, transistors).
    • Density: ROM’s matrix design (below) packs more bits than latch-based SRAM, critical for larger memories.

In short, D latches are ideal for RAM’s read/write needs but overkill for ROM’s fixed, read-only data. ROM uses physical or programmable structures to encode 1s and 0s directly.

---

Internal Design of ROM

ROM’s internal architecture depends on its type (mask ROM, PROM, EPROM, EEPROM), but all share a decoder-matrix structure. I’ll explain the general design and focus on EEPROM, with notes on others for context.

1. Basic ROM Structure

A ROM is organized as:

• Address Decoder: Converts input address (e.g., 8 bits, A7–A0) into a selected word line (one of 256 rows).
• Memory Array: A grid where each row (word) stores a data word.
• Output Lines: Data bits (D0–D15) driven by the selected row’s contents.

2. ROM Types and Their Storage

Here’s how different ROMs encode bits in the memory array, explaining why latches aren’t used:

• Mask ROM:
  • Design: Bits are fixed during manufacturing.
  • Storage: Uses a diode matrix or transistor matrix.
    • Diode Matrix:
      • Grid of word lines (rows) and bit lines (columns).
      • A diode at an intersection (row i, column j) encodes a 1; no diode encodes a 0.
    • Transistor Matrix: NMOS/PMOS transistors act as switches (1 = transistor present, 0 = absent).
  • Use Case: Not for you (fixed at fab), but shows ROM’s static nature.
• PROM (Programmable ROM):
  • Design: One-time programmable by user.
  • Storage: Fusible links (e.g., nichrome fuses).
    • Each intersection has a fuse (initially 1).
    • Programming: Blow fuses (apply high current) to set 0s.
  • Use Case: Rare now, less practical than EEPROM for your project.
• EPROM (Erasable PROM):
  • Design: Reprogrammable via UV erasure.
  • Storage: Floating-gate MOSFETs.
    • Each bit is a MOSFET with a floating gate (no connection to external circuit).
    • 1 (Erased): No charge on gate, transistor conducts (bit line pulled low).
    • 0 (Programmed): High voltage (e.g., 25V) traps electrons on gate, blocking conduction (bit line stays high).
    • Programming: Apply high voltage to select rows/columns, setting 0s.
    • Erasure: UV light removes charge, resetting to 1s.
  • Use Case: Viable, but needs UV programmer/eraser.
• EEPROM (Electrically Erasable PROM):
• Design: Reprogrammable electrically, ideal for your ROM (256 × 16 bits).
• Storage: Floating-gate MOSFETs with tunneling.
  • Similar to EPROM, but adds a thin oxide layer for Fowler-Nordheim tunneling.
  • 1: No charge, transistor conducts.
  • 0: Charge trapped via tunneling (high voltage, ~12V).
  • Programming: Apply voltage to set 0s, reverse to erase to 1s, byte-by-byte.
• Use Case: Perfect for you.

-end-

My Summary

In the previous entry, Grok suggested that we use a ROM (an EEPROM more specifically) to "store control signals for the instruction decoder". Grok suggests that we use a "256 x 16 ROM". This means that it has 256 addresses, where each address can store 16 bits, bit 0 to bit 15:

Such a ROM will have 8 input pins for the address (2^8 = 256) and 16 output pins for the data. This is the symbol I will use:

We simply set an address, say 0110 1100 on the input pins and the 16 output pins will hold a 0 or a 1 depending on how we have programmed the ROM. The ROM really acts as a "look-up table". The actual data held by the ROM will be the "control signals", but not sure precisely how yet - will get back to this.

Here is a example of an EEPROM, ATMELs AT28C64B:

This EEPROM has a 13 bit address (13 of the pins are input pins A0-A12), with a total of 2^13 = 8192 addresses, way more than we need right now. This is not a problem though. We use only A0-A7 and set the 5 highest pins, A8-A12, to 0.

AT28C64B stores only 8 bits at each address (it has 8 output pins). The simplest solution is to use two of these, one for the first 8 data bits and one for the remaining 8 data bits. In addition to the 21 address and data pins, it has pins to control if we are writing data to the ROM or reading data from the ROM.

ACEL ROM

I created a 256 x 16 ROM in ACEL, called "ROM256x16". To "program" this ROM, we define a variable called "data" (you can name it whatever you want):

        uint16_t data[256] = {"data at A=0", "data at A=1", "data at A=2",...};

"data" is an array of 256 "uint16_t", where "uint16_t" means 16 bits. This is precisely what we need to program the ROM. For example, if we do

        uint16_t data[256] = {0b0000000000000000, 0b1000000000000011};

then all bits at address 0 will be set to 0. At address 1, bit 0 (left-most bit) will be set to 1, bit 14 and bit 15 will be set to 1, and the rest to 0. Since we have not defined any data for address 2 and onwards, they will all be set to 0 (all bits 0).

Now, programming RAM by typing each individual bit is not the best way. Instead, we break up the sixteen binary bits into four groups of four bits each. For example,

        1000 0000 0000 0011

Each group of four binary digits is then converted to a single hex digit (see entry 9): 

        1000 0000 0000 0011 = 8003 in hex

An equivalent, but simpler way of programming RAM is as follows (where the "x" indicates hex)

        uint16_t data[256] = {0x0000, 0x8003};

Conversion between hex and binary is super simple. You can program the ROM using decimal numbers as well, but the conversion between binary and decimal is "messy". Using a converter, for example Windows Calculator, we see that 1000 0000 0000 0011 is 32771 in decimal.

Therefore, we can also write

        uint16_t data[256] = {0, 32771};

Finally, we initialize the chip "ROM256x16" with the data. 

        auto* rom = new ROM256x16(data);

You can test it on Wokwi, project "256 x 16 ROM". 

Next, let's figure out how to use the ROM to store control signals... in the next entry.

Entry 29: T-states and control signals

Introduction

In the previous entry, we looked at instructions and the instruction register. The current goal is to build a processor that can run the following program:

This program adds 5 and 3 and displays the result on LEDs. Also, we decided that the processor should support the following instructions:

In order to support these instructions, we need the following components (as a starting point):

• See entry 26 and 27 for the program counter
• See entry 21 for the memory system
• See entry 28 for the instruction register

"A, B, OUT and ALU" (see entry 23):

Here is a summary of all the control pins we need to implement the 8 instructions above (in parenthesis, action when pin is high):

• Program counter:
• COUNT (increase count)
• PCL (loads from the data bus)
• PCW (writes to the address bus)
• Memory system:
• MARL (loads MAR from the address bus)
• MDRL (loads MDR from the data bus)
• RAML (loads data stored in MDR at address stored in MAR into RAM)
• RAMW (writes data to data bus and address bus)
• Instruction register
• IRL (loads from the data bus)
• A, B, OUT and ALU
• RAL (loads register A from the data bus)
• RBL (loads register B from the data bus)
• ROL (loads register OUT from the data bus and activates LEDs)
• RAW (writes A to the data bus)
• ALUW (writes ALU to the data bus)

The next step is to build an "instruction decoder" so that the processor can "run the program" by itself. 

I didn't really follow the first answer by Grok on "instruction decoding" but the concept "T-state" was mentioned. So, let's start there.

T-states

"Is the instruction decoder related to "T states"? Grok:

Your question about whether the instruction decoder is related to T-states is spot-on, and it ties directly into how instructions are executed in a system like yours. Let’s break it all down, clarify the role of the instruction decoder, explain T-states, and design a decoder for your eight instructions (NOP, LDA, ADD, STA, JMP, HLT, MOV B, A, MOV OUT, A).

Instruction Set (Proposed): (Removed, see table above)

Instruction Format:

• NOP, ADD, HLT, MOV B,A, MOV OUT,A: Single 4-bit opcode (4 bits total).
• LDA, STA, JMP: Opcode + 4-bit address (8 bits, two fetches).

What Are T-States?

• Definition: A T-state (Timing state) is one clock cycle in a processor’s operation, representing the smallest unit of time for executing part of an instruction. In the 8085, each instruction takes multiple T-states (e.g., LDA 2034H = 13 T-states), split across fetch, decode, and execute phases.
• Purpose: T-states break down instruction execution into steps:
• Fetch opcode from RAM.
• Fetch operands (e.g., address for LDA).
• Decode opcode.
• Execute (e.g., load, add, store).

Instruction Decoder and T-States

• Relation: The instruction decoder is intimately tied to T-states because it generates control signals that determine what happens in each T-state (e.g., clocking IR, enabling ALU, writing RAM). Each instruction requires a specific sequence of T-states, and the decoder ensures the right signals are active at the right time.

My summary

This is my summary, after feedback from Grok. It is a long summary, but this is the "gist" of the processor.

• Each instruction requires a number of T-states to complete. For example, an instruction needing 4 T-states takes four clock cycles to execute.
• T-states start with T-state 1, followed by T-state 2, and so on. After the final T-state, the processor returns to T-state 1 to fetch the next instruction.
• In each T-state, relevant control pins (or, as they are also called, control signals) are set to perform specific actions, remaining stable throughout the T-state and changing at the start of the next.
• A T-state begins on the clock’s falling edge (high-to-low from the 555 timer) and lasts until the next falling edge, ensuring that the control pins remain stabilized on the clock's rising edge (low-to-high). In this example, instruction 1 has 4 T-states and instruction 2 has 3 T-states:

• For example, to move Register A’s contents to Register B in one T-state, the decoder enables A’s "Write" pin (RAW) and B’s "Load" pin (RBL) on the clock’s falling edge. A's data immediately goes on the data bus. However, B latches the data first on the following clock’s rising edge. This gives register A plenty of time to put the data onto the bus, ensuring a valid transfer. 

• T-state 1 is identical for all instructions. The Instruction Register (IR) doesn’t yet hold the opcode. Control signals are set to transfer the Program Counter (PC) value to the Memory Address Register (MAR). The decoder sets PCW = 1 (PC writes to the address bus), and MARL = 1 (MAR loads from the address bus).
• T-state 2 is also universal. Here, the opcode is moved from RAM to the IR, and the PC is incremented. RAM already has the correct address, due to T-state 1. Therefore, in T-state 2, the decoder sets RAMW = 1 (RAM writes data to both buses), IRL = 1 (IR loads from the data bus), and COUNT = 1 (PC increments its count).
• T-state 3 and beyond depend on the opcode in the IR. For NOP, T-state 3 is idle, and the processor returns to T-state 1 for the next instruction’s fetch.
• For MOV B,A, T-state 3 sets RAW = 1 and RBL = 1 as discussed in the example above. No further action is needed, so it returns to T-state 1 for the next instruction.
• Thus, for all eight instructions—NOP, LDA, ADD, STA, JMP, HLT, MOV B, A, MOV OUT, A—we define how the decoder sets control signals in T-state 3 onward, while T-states 1 and 2 are uniformly handled.

Here is a complete list of control signals for all instructions in all T-states:

T-state 1: move the program count to MAR. T-state 2: move the opcode to IR and increase PC.

For example, consider STA. Since the PC was incremented in T-state 2, it is now pointing at the address at which to store the A register. So we move this address to MAR in T-state 3. In T-state 4, the decoder sets RAML = 1 and RAM will immediately load the data found in MDR into the correct address (the address in MAR). This is not the correct data, but that is OK. It also sets RAW = 1 so that the A register goes on the data bus. Since is sets MDRL = 1, MDR will load the correct data on the rising clock edge. RAM will then immediately write this (correct data) into the correct address. COUNT = 1 so the the PC increments, it will now point at the next opcode.

The next question is then, how do we build an instruction decoder which, depending on T-state and instruction, sets the correct control signals? Grok:

You can use ROM to store control signals for the instruction decoder, based on the current T-state and opcode. It aligns perfectly with how many real-world microprogrammed CPUs implement their control units. By using a ROM to map T-states and opcodes to control signals, you can centralize the instruction decoder’s logic, making it easier to modify or expand your 4-bit processor. In essence, ROM is a lookup table. Let’s explore why this works, design the ROM-based decoder, calculate its size, and define the control signals.

Next, let's figure out how ROM differs from RAM and then design the instruction decoder. Hopefully we can then make the processor run programs, like the one above.. in the next entry.

Entry 28: Instruction register

Instructions 

"Can you tell me about instructions, instruction register and instruction decoder?". Groks (curated) response:

Your setup is incredibly impressive—a fully functional 4-bit... (describing what we have so far). Adding instructions, an instruction register (IR), and an instruction decoder is the next logical step to turn your system into a basic processor capable of executing a program. Let’s dive into what these components are, how they work, and how you can integrate them into your setup to start running simple instructions.

---

What Are Instructions?

• Definition: Instructions are the basic commands a processor executes, encoded as binary patterns stored in memory (your RAM). Each instruction tells the system what to do, like load data, add numbers, or jump to a new address.
• In Your System: Instructions are 4-bit values (since your data bus is 4 bits), stored in the 16x4 RAM, addressed by the 4-bit PC (0000 to 1111).
• Purpose: Define a program—e.g., load Register A, add to B, store result—executed sequentially or with jumps.
• Example Instructions (4-bit):
  • 0001: Load A from RAM.
  • 0010: Add A and B, store in A.
  • 0011: Store A to RAM.

Instruction Format

• 4 Bits: Limited to 16 unique instructions (0000 to 1111).
• Encoding: Each 4-bit code maps to an operation (opcode). Some instructions might include a 4-bit address (requiring a second fetch).
• Simple Set (Proposed):
  • 0000: NOP (no operation).
  • 0001: LDA addr (load A from RAM[addr]).
  • 0010: ADD (A = A + B).
  • 0011: STA addr (store A to RAM[addr]).
  • 0100: JMP addr (set PC to addr).
  • 0101: HLT (halts the program)
  • 0110: MOV B, A (move A to B)
  • 0111: MOV OUT, A  (move A to OUT)
  • More later as needed.

Example Program

Store in RAM:

• 0000: 0001 (LDA 1000)
• 0001: 1000 (address 1000)
• 0010: 0110 (MOV B, A)
• 0011: 0001 (LDA 1001)
• 0100: 1001 (address 1001)
• 0101: 0010 (ADD)
• 0110: 0111 (MOV B, OUT)
• 0111: 0101 (HLT)
• 1000: 0101 (data: 5)
• 1001: 0011 (data: 3)

---

My summary

• An instruction tells the processor what to do. For example, "LDA 6" means "Load the register A with whatever number is found at address 6" and "ADD" means "Add the numbers in register A and B and put the sum in register A".
• It is up to us to define which instructions the processor must understand, but the processor’s hardware (decoder, ALU, etc.) must support these instructions. 
• Some instructions "stand by themselves" (they are "single-word instructions"). These are "NOP", "ADD", "HLT", MOV B, A, and MOV OUT, A. 
• Some instructions have an "operand". For example, "LDA" by itself would be pointless. Therefore, it has an operand, which is a four bit address from which to get the number to put in A. STA and JMP also have an address as an operand. 
• NOP, ADD, HLT, LDA, STA, JMP, MOV B, A, and MOV OUT, A are called opcodes. Each opcode is represented by a four bit binary number. NOP by 0000, LDA by 0001, ADD by 0010, and so on.
• Instructions that stand by themselves occupy one address in RAM. The data at this address is simply the four bit binary representation of the opcode.
• Instructions with an operand occupy two addresses in RAM. The first one is the opcode and the second one is the address.
• This means that a number stored in RAM at a given address can mean many things. It can be an opcode, it can be an operand (address), and it can be data.

I did confirm this summary with Grok and the summary includes comments made by Grok. Here is a summary of the eight instructions that Grok suggests we start with:

Let's have a closer look at the example program, repeated here with some more details:

This program will add 5 and 3 and display the result, in binary, using 4 LEDs. When we start the "computer", PC is zero and the processor will execute the first instruction, "LDA 8", loading register A with the number 5. It will then move on to the next instruction, "MOV B,A". It keeps on going until it gets to address 7 and "HLT". Note that addresses 0 to 7 is used for code while addresses 8 and 9 is used for data.

All of this is so far "in theory". What we have so far cannot decode instruction. Let's move on to the instruction register.

Instruction register

What Is an Instruction Register (IR)?

• Definition: The IR is a register that temporarily holds the current instruction (opcode) fetched from RAM during execution.
• Purpose:
  • Stores the 4-bit instruction after it’s read from RAM (via the data bus).
  • Feeds the instruction decoder to generate control signals.
• In Your System: A 4-bit register to hold the opcode, clocked when fetching from RAM.

How It Works

• PC outputs address (e.g., 0001) to RAM via address bus.
• RAM outputs instruction (e.g., 0010 = ADD) to data bus.
• IR clocks, latching 0010 from data bus.
• IR Q0–Q3 stay stable, driving the decoder.

---

What Is an Instruction Decoder?

(I removed this for now. For me, this was too difficult to understand.)

-end-

Adding an instruction register

Let's add an instruction register (IR). This is "just a regular register", see entry 15. But it has a special purpose: it will hold the next opcode. This setup is sufficient to experiment with IR:

We enter the program using the DIPs:

• Addr: Data
• 0000: 0001 
• 0001: 1000 
• 0010: 0110 
• 0011: 0001 
• 0100: 1001 
• 0101: 0010 
• 0110: 0111 
• 0111: 0101 
• 1000: 0101 
• 1001: 0011 

Set AS and DS to ON to enter programming mode. Set address = 0000 and data = 0001 and click on "Load RAM", move on to address 1, and so on, until the program / data has been stored in RAM. Now, there is a way of cheating if we use ACEL. We can define 

    byte data[16] = {1,8,6,1,9,2,7,5,5,3,0,0,0,0,0,0};

and then we initialize the memory system with this data:

    auto* memorySys = new SixteenByFourMemorySystem(data);

But this is indeed cheating. If we were using real ICs, this would not be possible. We would have to program using the DIPs.

Try this out at Wokwi, project "Instruction Register":

This project is very similar to "Program counter and memory system", see entry 17. The only difference is that the OUT register is replaced by an instruction register. Try the following steps:

We want to move the opcodes to the IR

  1. Move the content of PC to MAR (address = 0 in RAM)

  2. Move the content of RAM at address 0 (the number 1) to the IR. IR now holds 0001 or "LDA"

  3. Increment PC twice

  4. Move the content of PC to MAR (address = 2 in RAM)

  5. Move the content of RAM at address 2 (number 6) to the IR. IR now holds 0110 or "MOV B,A"

  6. Increment PC

  7. Move the content of PC to MAR (address = 3 in RAM)

  8. Move the content of RAM at address 3 (the number 1) to the IR. IR now holds 0001 or "LDA"

  9. Continue until IR holds 0101 or "HLT"

    Click Print. Observe RAM and that correct data has been programmed.

    Move the first instruction:

      Click and hold PCW, MARL (press 3 and 5 on keyboard)

      Click Clock to latch

      Click and hold RAMW, IRL (press 7 and 8 on keyboard)

      Click Clock to latch

      Observe LEDs: 0001 means LDA

    Move the second instruction:

      Click and hold COUNT (4)

      Click Clock to latch twice

      Click and hold PCW, MARL (press 3 and 5 on keyboard)

      Click Clock to latch

      Click and hold RAMW, IRL (press 7 and 8 on keyboard)

      Click Clock to latch

      Observe LEDs: 0110 means MOV B,A

    Move the remaining instructions to the IR.

    Increment count by 1 or 2 depending on the opcode

The next step is to "decode" the instructions. This process is related to concept "T-state"... in the next entry.

Entry 27: Program counter and memory system

Testing the program counter and the memory system

We designed the program counter in entry 26. Let's hook it up to the address bus and to the memory system to make sure that these two component can interact. This is what I want to test:

1. Incrementing the program counter (PC)
2. Sending the the value of the PC to the Memory Address Register (MAR) over the address bus
3. Updating the PC by sending a new address from RAM to the PC over the data bus.

I also add a new OUT register The purpose of this register is to display the result of whatever operation the computer has performed. I will hook it up like this:

I will use the following four control pins on the PC:

• Count (Count = 1 will increase count when Clock goes high): COUNT
• Write (Write = 1 enables W and puts count on address bus): PCW
• Load (Load = 1 sets the count to the value on the data bus D): PCL

I will also use the Load control pin on the OUT register: OUTL. The memory system was designed in entry 21:

I will use the two S-pins of the two MUX's, AS and DS, to set if we are in "programming mode" (programming RAM with the DIP's) or in "computing mode", where RAM takes address and data from the busses, via MAR and MDR. I will also use the following 5 control pins (and names):

• Load on MAR (Load = 1 loads the address from the address bus, which is then the address seen by RAM if it is in computing mode): MARL.
• Load on RAM (Load = 1 loads the data on D pins into RAM at address A): RAML.
• Write on RAM (Write = 1 writes the data at address A to the buses): RAMW.

Try it out on Wokwi: Project "Testing Program counter with memory system". On Wokwi, you can see which chips that are used and the connections that are made.

Step by step instructions to perform the test:

  Testing the Program counter with the memory system

  1. Use the DIP switches to program RAM.

      Put 8 at address 1 and 15 at address 8.

  2. Increase the count in the program counter (PC) (making it equal to 1)

  3. Move the content of PC to MAR so that address is 1 in RAM

  4. Move the content of RAM at address 1 (the number 8) to the PC

  5. Move the content of PC to MAR so that address is 8 in RAM

  6. Move the content of RAM at address 8 (the number 15) to the OUT register

  Step by step:

    Set DIP 1 to ON on the address DIP's (left)

    Set DIP 1 to ON on the data DIP's (right)

    This takes us into "programming mode" where the DIPs determine address and data  

    Program: 8 at address 1, 15 at address 8:

      Set address DIPs to 0001

      Set data DIPS to 1000 (decimal 8)

      Click RAML

      Similarly for address 8 (address: 1000, data: 1111)

    Click Print. Observe RAM and that correct data has been programmed.

    Return to "compute mode" by setting both DIP 1's to OFF

    Increment PC

      Click and hold COUNT (press 4 on keyboard)

      Click Clock to latch

      Click Print. Observe Q = 1 in program counter.

    Move the content of PC to MAR

      Click and hold PCW, MARL (press 3 and 5 on keyboard)

      Click Clock to latch

      Click Print. Observe MAR Q = 1, RAM Address = 1 and RAMQ = 8

    Move the content of RAM at address 1 to the PC

      Click and hold RAMW, PCW (press 2 and 7 on keyboard)

      Click Clock to latch

      Click Print. Observe PC Q = 8

    Move the content of PC to MAR

      Click and hold PCW, MARL (press 3 and 5 on keyboard)

      Click Clock to latch

      Click Print. Observe MAR Q = 8, RAM Address = 8 and RAMQ = 15

    Move the content of RAM at address 8 to the output register

      Click and hold RAMW, OUTL (press 7 and 8 on keyboard)

      Click Clock to latch

    Observe LED bar displays 1111 (15)

Let's move on to programming this stupid thing... in the next entry.

Entry 26: Four bit program counter

In entry 24, we designed a T flip-flop, which functions as a 1 bit binary counter:

Making the 1 bit counter Loadable

The next step is to make it possible to "Load" a value into the counter. To do this, we use the Preset and Clear pins. Let's denote the value we want to load by "D":

• If we are loading the counter and D = 0, Clear should be 1 (and Preset = 0)
• If we are loading the counter and D = 1, Preset should be 1 (and Clear = 0)
• If we are not loading the counter,  Preset and Clear should both be 0.

This is easy to do, no need to consult Grok:

Let's use the following symbol for the "loadable" T flip-flop:

To review:

• When L = 1, Q becomes equal to D (no clock involved)
• When L = 0, D is ignored. It then counts when T = 1 and Clock goes high.

4 bit counter

Let's look at the binary numbers between 0 and 3:

We use a T flip flop for the right-most binary digit (the lowest order), called T0. We also use a T flip-flop for the second binary digit from the right, called T1. However, T1 should only count when T0 becomes 0. This is easy to do: we simply connect Q-bar from T0 to the clock signal of T1. Now T1 will increment when T0 goes from 1 to 0, but not when it goes from 0 to 1.

Similarly, we use a T flip-flop for the third and the fourth binary digit from the right, T2 and T2. Q-bar from T1 is connected to the clock of T2, and Q-bar from T2 is connected to the clock of T3. This will result in a loadable 4 bit counter:

• It contains 4 T flip-flop, T0 to T3, holding binary digits Q0 to Q3. The four bit binary number is Q3_Q2_Q1_Q0.
• Input pin Clock. (goes to T0 clock)
• Input pin Count. When Count = 1, Q3_Q2_Q1_Q0 is incremented by 1 when clock goes high. When Count = 0, nothing happens when clock goes high.
• Input pin Load and input pins D0 to D3. When Load = 1, Q3_Q2_Q1_Q0 becomes equal to D3_D2_D1_D0. When Load = 0, D0 to D3 are ignored.
• Output pins Q0 to Q3. The count value hold by the counter. Note that Q0 is the lowest order bit and Q3 the highest.

Program counter

Two more issues before this is a program counter.

1. The output (count) Q should be hooked up to the address bus. Therefore, we also need four tri-state switches hooked up to Q0-Q3 resulting in W0-W3, tri-state output. This also comes with a "Write" pin that enables the switches.
2. A simpler way to set the count tp zero. It is already possible, by setting D0-D3 to 0000 and setting Load = 1. However, I want to add a control pin Clear, which when high, sets Q to 0. This is easy to do with an OR gate:

This is the symbol for my (for now) final program counter:

The name of this chip is "FourBitProgramCounter".

• D: four bits to set the count
• L: Load = 1 loads D
• C: Count = 1 will increase Q when Clock goes high
• Wr: Write = 1 enables tri-state, W = Q. When Write = 0, W = ZZZZ
• Cl: Clear = 1 sets Q = 0.

This chip is similar to 74LS193, the program counter suggested by Grok. Internally, they are designed differently. Also, 74LS193 can count downwards.

Testing the program counter

Here I have the "FourBitProgramCounter" in a Arduino Nano, together with a "SevenSegmentDecoderCathode", see entry 10. The clock signal from my 555 is connected to the Clock of the program counter. Count is set to 1 and the program counter Q is hooked up to the input pins of the decoder. I am not using any other pins on the counter. The output pins of the decoder are then connected to the display:

The green button is the "Print" button, printing the state of both the chips in the Nano.

You can try out the program counter on Wokwi as well ("Four bit program counter"). Here, you control the clock. In this project, Load and Clear are implemented. For example, you can try:

  Click the clock pin repeatedly.

  Observe that the count on the display increases by 1 when the clock goes high.

  Remember, A=10, b = 11, C = 12, d = 13, E = 14, F = 15

  Make the count 15 (F) and click Clock

  Observe that the count goes back to zero.

  Click Clear and observe that count becomes zero.

  Set a number on the DIPs 5-8, for example 0101 (5) and click Load.

  Observe that count becomes 5.

I want to hook up the program counter to the memory system... in the next entry.

Entry 25: Automatic clock

In the previous entry, we designed a 1 bit counter using a T flip-flop. If the clock signal goes on and off (while T = 1) continuously, you will observe the following:

Try this out yourself on Wokwi, "T flip-flop". In order to see this more clearly, I want to create an "automatic" clock signal, relieving me from the work of clicking the button. Let's do this before we create a 4 bit counter.

Automatic clock signal

"How do you create an automatic clock signal?"

Creating an automatic clock signal for your 4-bit synchronous program counter (or any digital circuit) is a great way to move from manual button presses to continuous operation, mimicking a real CPU’s clock. An automatic clock generates a steady stream of pulses (square waves) at a predictable frequency, toggling between 0 and 1 to drive your system. The simplest and most popular method is using a 555 timer IC in astable mode, which produces a continuous oscillating signal without external triggering. Since you’ve been working with TTL (74LS series) components, we’ll design it to output a 5V-compatible square wave at a frequency suitable for manual observation or faster testing. Let’s walk through it step-by-step.

---

Why an Automatic Clock?

• Manual CLK (Button): Your current CPU signal relies on button presses—slow and irregular (~1 Hz if you’re fast).
• Automatic CLK: A 555 timer provides a consistent, adjustable frequency (e.g., 1 Hz to 10 kHz), letting your counter increment automatically and your system run like a real processor.

---

The 555 Timer in Astable Mode

• Function: In astable mode, the 555 timer oscillates continuously, producing a square wave at its output (Pin 3).
• Key Features:
  • Frequency and duty cycle set by resistors and a capacitor.
  • TTL-compatible output (0V to ~5V with proper setup).

---

-end-

The 555 is a fairly simple chip, but it cannot be designed from basic gates. It contains an SR latch that holds the state (0 or 1), and some additional transistors and resistors. Just like the basic gates and the tri-state switch, I will not dig into the "transistor-details". In addition to the 555 chip, you also need a few resistors and capacitors. This is what I use:

Here it is hooked up to an LED:

Clock signal to T flip-flop

I am hooking up the clock signal from my 555 board to a T flip-flop:

The purple box represents the clock signal. Here is the result:

Observe how the frequency of the output is precisely half the frequency of the clock signal, just like in the picture at the top. You can try this out yourself at Wokwi, project "Clock to T flip-flop". On to the 4-bit program counter, in the next entry.